This article introduces the basic concepts of binary trees, and then works through a series of practice problems with solution code in C/C++ and Java. Binary trees have an elegant recursive pointer structure, so they are a good way to learn recursive pointer algorithms.

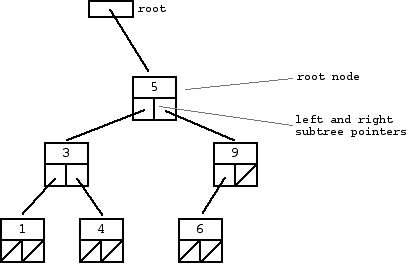
A "binary search tree" (BST) or "ordered binary tree" is a type of binary tree where the nodes are arranged in order: for each node, all elements in its left subtree are less-or-equal to the node (<=), and all the elements in its right subtree are greater than the node (>). The tree shown above is a binary search tree -- the "root" node is a 5, and its left subtree nodes (1, 3, 4) are <= 5, and its right subtree nodes (6, 9) are > 5. Recursively, each of the subtrees must also obey the binary search tree constraint: in the (1, 3, 4) subtree, the 3 is the root, the 1 <= 3 and 4 > 3. Watch out for the exact wording in the problems -- a "binary search tree" is different from a "binary tree".
The nodes at the bottom edge of the tree have empty subtrees and are called "leaf" nodes (1, 4, 6) while the others are "internal" nodes (3, 5, 9).
For each problem, there are two things to understand...
In C or C++, the binary tree is built with a node type like this...
struct node {
int data;
struct node* left;
struct node* right;
}
/*
Given a binary tree, return true if a node
with the target data is found in the tree. Recurs
down the tree, chooses the left or right
branch by comparing the target to each node.
*/
static int lookup(struct node* node, int target) {
// 1. Base case == empty tree
// in that case, the target is not found so return false
if (node == NULL) {
return(false);
}
else {
// 2. see if found here
if (target == node->data) return(true);
else {
// 3. otherwise recur down the correct
subtree
if (target < node->data) return(lookup(node->left,
target));
else return(lookup(node->right,
target));
}
}
}
The lookup() algorithm could be written as a while-loop that iterates down the tree. Our version uses recursion to help prepare you for the problems below that require recursion.
// suppose the variable "root" points to the tree
root = change(root);
We take the value returned by change(), and use it as the new value for root. This construct is a little awkward, but it avoids using reference parameters which confuse some C and C++ programmers, and Java does not have reference parameters at all. This allows us to focus on the recursion instead of the pointer mechanics. (For lots of problems that use reference parameters, see CSLibrary #105, Linked List Problems, http://cslibrary.stanford.edu/105/).
2
/ \
1 10
returns the tree...
2
/ \
1 10
/
5
The solution shown here introduces a newNode() helper function that builds a single node. The base-case/recursion structure is similar to the structure in lookup() -- each call checks for the NULL case, looks at the node at hand, and then recurs down the left or right subtree if needed.
/*
Helper function that allocates a new node
with the given data and NULL left and right
pointers.
*/
struct node* NewNode(int data) {
struct node* node = new(struct node);
// "new" is like "malloc"
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
/*
Give a binary search tree and a number, inserts a new node
with the given number in the correct place in the tree.
Returns the new root pointer which the caller should
then use (the standard trick to avoid using reference
parameters).
*/
struct node* insert(struct node* node, int data) {
// 1. If the tree is empty, return a new, single node
if (node == NULL) {
return(newNode(data));
}
else {
// 2. Otherwise, recur down the tree
if (data <= node->data) node->left = insert(node->left,
data);
else node->right = insert(node->right, data);
return(node); // return the (unchanged) node
pointer
}
}
The shape of a binary tree depends very much on the order that the nodes are inserted. In particular, if the nodes are inserted in increasing order (1, 2, 3, 4), the tree nodes just grow to the right leading to a linked list shape where all the left pointers are NULL. A similar thing happens if the nodes are inserted in decreasing order (4, 3, 2, 1). The linked list shape defeats the lg(N) performance. We will not address that issue here, instead focusing on pointers and recursion.
Reading about a data structure is a fine introduction, but at some point the only way to learn is to actually try to solve some problems starting with a blank sheet of paper. To get the most out of these problems, you should at least attempt to solve them before looking at the solution. Even if your solution is not quite right, you will be building up the right skills. With any pointer-based code, it's a good idea to make memory drawings of a a few simple cases to see how the algorithm should work.
2
/ \
1 3
Write the code in three different ways...
struct node* build123() {
int size(struct node* node) {
int maxDepth(struct node* node) {
int minValue(struct node* node) {
4
/ \
2 5
/ \
1 3
Produces the output "1 2 3 4 5". This is known as an "inorder" traversal of the tree.
Hint: For each node, the strategy is: recur left, print the node data, recur right.
void printTree(struct node* node) {
4
/ \
2 5
/ \
1 3
Produces the output "1 3 2 5 4". The description is complex, but the code is simple. This is the sort of bottom-up traversal that would be used, for example, to evaluate an expression tree where a node is an operation like '+' and its subtrees are, recursively, the two subexpressions for the '+'.
void printPostorder(struct node* node) {
5
/ \
4 8
/
/ \
11
13 4
/ \
\
7
2 1
Root-to-leaf paths:
path 1: 5 4 11 7
path 2: 5 4 11 2
path 3: 5 8 13
path 4: 5 8 4 1
For this problem, we will be concerned with the sum of the values of such a path -- for example, the sum of the values on the 5-4-11-7 path is 5 + 4 + 11 + 7 = 27.
Given a binary tree and a sum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum. Return false if no such path can be found. (Thanks to Owen Astrachan for suggesting this problem.)
int hasPathSum(struct node* node, int sum) {
Given a binary tree, print out all of its root-to-leaf paths, one per line.
void printPaths(struct node* node) {
So the tree...
4
/ \
2 5
/ \
1 3
is changed to...
4
/ \
5 2
/ \
3 1
The solution is short, but very recursive. As it happens, this can be accomplished without changing the root node pointer, so the return-the-new-root construct is not necessary. Alternately, if you do not want to change the tree nodes, you may construct and return a new mirror tree based on the original tree.
void mirror(struct node* node) {
So the tree...
2
/ \
1 3
is changed to...
2
/ \
2 3
/ /
1 3
/
1
As with the previous problem, this can be accomplished without changing the root node pointer.
void doubleTree(struct node* node) {
int sameTree(struct node* a, struct node* b) {
Suppose you are building an N node binary search tree with the values 1..N. How many structurally different binary search trees are there that store those values? Write a recursive function that, given the number of distinct values, computes the number of structurally unique binary search trees that store those values. For example, countTrees(4) should return 14, since there are 14 structurally unique binary search trees that store 1, 2, 3, and 4. The base case is easy, and the recursion is short but dense. Your code should not construct any actual trees; it's just a counting problem.
int countTrees(int numKeys) {
a. 5 -> TRUE
/ \
2 7
b. 5 -> FALSE, because the 6 is not ok to the
left of the 5
/ \
6 7
c. 5 -> TRUE
/ \
2 7
/
1
d. 5 -> FALSE, the 6 is ok with the 2, but the
6 is not ok with the 5
/ \
2 7
/ \
1 6
For the first two cases, the right answer can be seen just by comparing
each node to the two nodes immediately below it. However, the fourth case
shows how checking the BST quality may depend on nodes which are several
layers apart -- the 5 and the 6 in that case.
Returns true if a binary tree is a binary search tree.
int isBST(struct node* node) {
/*
Returns true if the given tree is a binary search tree
(efficient version).
*/
int isBST2(struct node* node) {
return(isBSTRecur(node, INT_MIN, INT_MAX));
}
/*
Returns true if the given tree is a BST and its
values are >= min and <= max.
*/
int isBSTRecur(struct node* node, int min, int max) {
root->left = lChild;
root->right= rChild;
return(root);
}
// call newNode() three times, and use only one local variable
struct node* build123b() {
struct node* root = newNode(2);
root->left = newNode(1);
root->right = newNode(3);
return(root);
}
/*
Build 123 by calling insert() three times.
Note that the '2' must be inserted first.
*/
struct node* build123c() {
struct node* root = NULL;
root = insert(root, 2);
root = insert(root, 1);
root = insert(root, 3);
return(root);
}
// use the larger one
if (lDepth > rDepth) return(lDepth+1);
else return(rDepth+1);
}
}
// loop down to find the leftmost leaf
while (current->left != NULL) {
current = current->left;
}
return(current->data);
}
printTree(node->left);
printf("%d ", node->data);
printTree(node->right);
}
// first recur on both subtrees
printTree(node->left);
printTree(node->right);
// then deal with the node
printf("%d ", node->data);
}
Strategy: subtract the node value from the sum when recurring
down,
and check to see if the sum is 0 when you run out of tree.
*/
int hasPathSum(struct node* node, int sum) {
// return true if we run out of tree and sum==0
if (node == NULL) {
return(sum == 0);
}
else {
// otherwise check both subtrees
int subSum = sum - node->data;
return(hasPathSum(node->left, subSum) ||
hasPathSum(node->right,
subSum));
}
}
printPathsRecur(node, path, 0);
}
/*
Recursive helper function -- given a node, and an array containing
the path from the root node up to but not including this
node,
print out all the root-leaf paths.
*/
void printPathsRecur(struct node* node, int path[], int pathLen)
{
if (node==NULL) return;
// append this node to the path array
path[pathLen] = node->data;
pathLen++;
// it's a leaf, so print the path that led to here
if (node->left==NULL && node->right==NULL) {
printArray(path, pathLen);
}
else {
// otherwise try both subtrees
printPathsRecur(node->left, path, pathLen);
printPathsRecur(node->right, path, pathLen);
}
}
// Utility that prints out an array on a line.
void printArray(int ints[], int len) {
int i;
for (i=0; i<len; i++) {
printf("%d ", ints[i]);
}
printf("\n");
}
So the tree...
4
/ \
2 5
/ \
1 3
is changed to...
4
/ \
5 2
/ \
3 1
*/
void mirror(struct node* node) {
if (node==NULL) {
return;
}
else {
struct node* temp;
// do the subtrees
mirror(node->left);
mirror(node->right);
// swap the pointers in this node
temp = node->left;
node->left = node->right;
node->right = temp;
}
}
So the tree...
2
/ \
1 3
Is changed to...
2
/ \
2 3
/ /
1 3
/
1
*/
void doubleTree(struct node* node) {
struct node* oldLeft;
if (node==NULL) return;
// do the subtrees
doubleTree(node->left);
doubleTree(node->right);
// duplicate this node to its left
oldLeft = node->left;
node->left = newNode(node->data);
node->left->left = oldLeft;
}
// 2. both non-empty -> compare them
else if (a!=NULL && b!=NULL) {
return(
a->data == b->data &&
sameTree(a->left, b->left) &&
sameTree(a->right, b->right)
);
}
// 3. one empty, one not -> false
else return(false);
}
Strategy: consider that each value could be the root.
Recursively find the size of the left and right subtrees.
*/
int countTrees(int numKeys) {
if (numKeys <=1) {
return(1);
}
else {
// there will be one value at the root, with
whatever remains
// on the left and right each forming their
own subtrees.
// Iterate through all the values that could
be the root...
int sum = 0;
int left, right, root;
for (root=1; root<=numKeys; root++) {
left = countTrees(root - 1);
right = countTrees(numKeys - root);
// number of possible trees with
this root == left*right
sum += left*right;
}
return(sum);
}
}
// false if the max of the left is > than us
// (bug -- an earlier version had min/max backwards here)
if (node->left!=NULL && maxValue(node->left) > node->data)
return(false);
// false if the min of the right is <= than us
if (node->right!=NULL && minValue(node->right) <=
node->data)
return(false);
// false if, recursively, the left or right is not a BST
if (!isBST(node->left) || !isBST(node->right))
return(false);
// passing all that, it's a BST
return(true);
}
/*
Returns true if the given tree is a BST and its
values are >= min and <= max.
*/
int isBSTUtil(struct node* node, int min, int max) {
if (node==NULL) return(true);
// false if this node violates the min/max constraint
if (node->data<min || node->data>max) return(false);
// otherwise check the subtrees recursively,
// tightening the min or max constraint
return
isBSTUtil(node->left, min, node->data) &&
isBSTUtil(node->right, node->data+1, max)
);
}
In Java, we will have a BinaryTree object that contains a single root pointer. The root pointer points to an internal Node class that behaves just like the node struct in the C/C++ version. The Node class is private -- it is used only for internal storage inside the BinaryTree and is not exposed to clients. With this OOP structure, almost every operation has two methods: a one-line method on the BinaryTree that starts the computation, and a recursive method that works on the Node objects. For the lookup() operation, there is a BinaryTree.lookup() method that the client uses to start a lookup operation. Internal to the BinaryTree class, there is a private recursive lookup(Node) method that implements the recursion down the Node structure. This second, private recursive method is basically the same as the recursive C/C++ functions above -- it takes a Node argument and uses recursion to iterate over the pointer structure.
// BinaryTree.java
public class BinaryTree {
// Root node pointer. Will be null for an empty tree.
private Node root;
/*
--Node--
The binary tree is built using this nested node class.
Each node stores one data element, and has left and
right
sub-tree pointer which may be null.
The node is a "dumb" nested class -- we just use it
for
storage; it does not have any methods.
*/
private static class Node {
Node left;
Node right;
int data;
Node(int newData) {
left = null;
right = null;
data = newData;
}
}
/**
Creates an empty binary tree -- a null root pointer.
*/
public void BinaryTree() {
root = null;
}
/**
Returns true if the given target is in the binary
tree.
Uses a recursive helper.
*/
public boolean lookup(int data) {
return(lookup(root, data));
}
/**
Recursive lookup -- given a node, recur
down searching for the given data.
*/
private boolean lookup(Node node, int data) {
if (node==null) {
return(false);
}
if (data==node.data) {
return(true);
}
else if (data<node.data) {
return(lookup(node.left, data));
}
else {
return(lookup(node.right, data));
}
}
/**
Inserts the given data into the binary tree.
Uses a recursive helper.
*/
public void insert(int data) {
root = insert(root, data);
}
/**
Recursive insert -- given a node pointer, recur down
and
insert the given data into the tree. Returns the new
node pointer (the standard way to communicate
a changed pointer back to the caller).
*/
private Node insert(Node node, int data) {
if (node==null) {
node = new Node(data);
}
else {
if (data <= node.data) {
node.left = insert(node.left,
data);
}
else {
node.right = insert(node.right,
data);
}
}
return(node); // in any case, return the new
pointer to the caller
}
root.left = lChild;
root.right= rChild;
}
/**
Build 123 using only one pointer variable.
*/
public void build123b() {
root = new Node(2);
root.left = new Node(1);
root.right = new Node(3);
}
/**
Build 123 by calling insert() three times.
Note that the '2' must be inserted first.
*/
public void build123c() {
root = null;
root = insert(root, 2);
root = insert(root, 1);
root = insert(root, 3);
}
private int size(Node node) {
if (node == null) return(0);
else {
return(size(node.left) + 1 + size(node.right));
}
}
private int maxDepth(Node node) {
if (node==null) {
return(0);
}
else {
int lDepth = maxDepth(node.left);
int rDepth = maxDepth(node.right);
// use the larger + 1
return(Math.max(lDepth, rDepth) + 1);
}
}
/**
Finds the min value in a non-empty binary search tree.
*/
private int minValue(Node node) {
Node current = node;
while (current.left != null) {
current = current.left;
}
return(current.data);
}
private void printTree(Node node) {
if (node == null) return;
// left, node itself, right
printTree(node.left);
System.out.print(node.data + " ");
printTree(node.right);
}
public void printPostorder(Node node) {
if (node == null) return;
// first recur on both subtrees
printPostorder(node.left);
printPostorder(node.right);
// then deal with the node
System.out.print(node.data + " ");
}
Strategy: subtract the node value from the sum when recurring
down,
and check to see if the sum is 0 when you run out of tree.
*/
public boolean hasPathSum(int sum) {
return( hasPathSum(root, sum) );
}
boolean hasPathSum(Node node, int sum) {
// return true if we run out of tree and sum==0
if (node == null) {
return(sum == 0);
}
else {
// otherwise check both subtrees
int subSum = sum - node.data;
return(hasPathSum(node.left, subSum) || hasPathSum(node.right,
subSum));
}
}
/**
Recursive printPaths helper -- given a node, and an array
containing
the path from the root node up to but not including this
node,
prints out all the root-leaf paths.
*/
private void printPaths(Node node, int[] path, int pathLen) {
if (node==null) return;
// append this node to the path array
path[pathLen] = node.data;
pathLen++;
// it's a leaf, so print the path that led to here
if (node.left==null && node.right==null) {
printArray(path, pathLen);
}
else {
// otherwise try both subtrees
printPaths(node.left, path, pathLen);
printPaths(node.right, path, pathLen);
}
}
/**
Utility that prints ints from an array on one line.
*/
private void printArray(int[] ints, int len) {
int i;
for (i=0; i<len; i++) {
System.out.print(ints[i] + " ");
}
System.out.println();
}
/**
Changes the tree into its mirror image.
So the tree...
4
/ \
2 5
/ \
1 3
is changed to...
4
/ \
5 2
/ \
3 1
Uses a recursive helper that recurs over the tree,
swapping the left/right pointers.
*/
public void mirror() {
mirror(root);
}
private void mirror(Node node) {
if (node != null) {
// do the sub-trees
mirror(node.left);
mirror(node.right);
// swap the left/right pointers
Node temp = node.left;
node.left = node.right;
node.right = temp;
}
}
So the tree...
2
/ \
1 3
Is changed to...
2
/ \
2 3
/ /
1 3
/
1
Uses a recursive helper to recur over the tree
and insert the duplicates.
*/
public void doubleTree() {
doubleTree(root);
}
private void doubleTree(Node node) {
Node oldLeft;
if (node == null) return;
// do the subtrees
doubleTree(node.left);
doubleTree(node.right);
// duplicate this node to its left
oldLeft = node.left;
node.left = new Node(node.data);
node.left.left = oldLeft;
}
/**
Recursive helper -- recurs down two trees in parallel,
checking to see if they are identical.
*/
boolean sameTree(Node a, Node b) {
// 1. both empty -> true
if (a==null && b==null) return(true);
// 2. both non-empty -> compare them
else if (a!=null && b!=null) {
return(
a.data == b.data &&
sameTree(a.left, b.left) &&
sameTree(a.right, b.right)
);
}
// 3. one empty, one not -> false
else return(false);
}
Strategy: consider that each value could be the root.
Recursively find the size of the left and right subtrees.
*/
public static int countTrees(int numKeys) {
if (numKeys <=1) {
return(1);
}
else {
// there will be one value at the root, with
whatever remains
// on the left and right each forming their
own subtrees.
// Iterate through all the values that could
be the root...
int sum = 0;
int left, right, root;
for (root=1; root<=numKeys; root++) {
left = countTrees(root-1);
right = countTrees(numKeys - root);
// number of possible trees with
this root == left*right
sum += left*right;
}
return(sum);
}
}
/**
Recursive helper -- checks if a tree is a BST
using minValue() and maxValue() (not efficient).
*/
private boolean isBST(Node node) {
if (node==null) return(true);
// do the subtrees contain values that do not
// agree with the node?
if (node.left!=null && maxValue(node.left) > node.data)
return(false);
if (node.right!=null && minValue(node.right) <=
node.data) return(false);
// check that the subtrees themselves are ok
return( isBST(node.left) && isBST(node.right) );
}
/**
Efficient BST helper -- Given a node, and min and max values,
recurs down the tree to verify that it is a BST, and that
all
its nodes are within the min..max range. Works in O(n) time
--
visits each node only once.
*/
private boolean isBST2(Node node, int min, int max) {
if (node==null) {
return(true);
}
else {
// left should be in range min...node.data
boolean leftOk = isBST2(node.left, min, node.data);
// if the left is not ok, bail out
if (!leftOk) return(false);
// right should be in range node.data+1..max
boolean rightOk = isBST2(node.right, node.data+1,
max);
return(rightOk);
}
}